Como epílogo a la ecuación del tiempo copiaré el código
Octave usado para obtener las gráficas de las entradas de la
ecuación del tiempo,
duración del día solar y
analema. Además ese código genera varias tablas con los datos numéricos calculados. La ruta empleada debería ajustarse según dónde tenga cada uno instalado
Octave. Hay un fichero principal, EDTinvocar_todo.txt, que llama a los demás. En
Octave la instrucción
source permite cargar y ejecutar un fichero. Basta hacer el
source del fichero principal, y las gráficas van saliendo con pausas entre ellas. Como mi experiencia con
Octave es limitada, es muy posible que la potencia de Octave se pueda usar de maneras mucho mejores, pero en el tema del plotting quizá sirvan los ejemplos, que en el manual de
Octave tampoco es que abunden, aunque es "la" referencia a consultar siempre. El código puede usarse libremente bajo la única responsabilidad de cada uno (at your own risk), sin ninguna garantía de que sea útil ni de que sea correcto, ni de que no perjudique la salud física o mental.
Disclaimer total.
Por cierto, para ver código fuente en el navegador, con las líneas largas ocupando una sola línea, es muy recomendable desactivar los estilos (suele ser en el menú Ver/Estilo).
EDTinvocar_todo.txt
#source("c:/octave/EDT/EDTinvocar_todo.txt");
source("c:/octave/EDT/EDTfunciones.txt");
source("c:/octave/EDT/EDTcalculo_principal.txt");
source("c:/octave/EDT/EDTgrafica_EDT_EEX_EIE.txt");pause(5);
source("c:/octave/EDT/EDTgrafica_lambda_alfa_gr.txt");pause(5);
source("c:/octave/EDT/EDTgrafica_M_nu_gr.txt");pause(5);
source("c:/octave/EDT/EDTgrafica_EDT_DiaSolar.txt");pause(5);subplot(1,1,1);
source("c:/octave/EDT/EDTgrafica_analema.txt");pause(2);
EDTfunciones.txt
#source("c:/octave/ecuTiempo.txt")
format long
global incliECLI=23.43928108*pi/180 #23°26'21".4119 (sin(incliECLI)=0.397776995) inclinación de la eclíptica
global anyotropico=365.242190402 # en días solares medios
global anyosidereo = 365.256363004 # en días solares medios, en la época J2000
global excentricidadTierra = 0.016729
global factorEDTsegrad = (24*60*60)/(2*pi) # escala vertical dif. angular (rad) <-> tiempo (s)
global factorEDTminrad = (24*60)/(2*pi) # escala vertical dif. angular (rad) <-> tiempo (min)
global omega_T = 2*pi / anyotropico # fecuencia angular del Sol Ecuatorial Medio, sistema equinoccial, rad/dia
global omega_S = 2*pi / anyosidereo # fecuencia angular de la anomalía media M, sistema orbital, rad/dia
global omega_P = omega_S*(1-(anyotropico/anyosidereo)); #frecuencia angular de precesión de los equinoccios, rad/dia
#{
La anomalía Excentrica E se calcula en base a la anomalía Media M,
y a la excentricidad e de la órbita, mediante la ecuación de Kepler
M = E - e sen(E)
#}
function ret = anomaliaExcentrica (anomaliaMedia, excentricidad)
fsol = @(x) (x - excentricidad *sin(x) - anomaliaMedia);
ret = fsolve(fsol,anomaliaMedia);
endfunction
#{
La anomalía verdadera, nu, se relaciona con la anomalia Excentrica E,
y la excentricidad e de la órbita, mediante
tan(nu/2)=sqrt( tan(E/2) * (1+e)/(1-e) )
Aqui se obtiene en función de la anomalía media M.
nu-M es periodica de periodo 2*pi.
Si M0=M-n*2*pi tal que 0<=M0<2*pi entonces
nu = nu0-M0+M = nu0 + n*2*pi
#}
function retv = anomaliaVerdadera (M, exc)
retv = zeros(1,length(M));
for i = [1:length(M)]
n = sign(M(i))*abs(floor(M(i)/(2*pi)));
M0=M(i)-n*2*pi;
E = anomaliaExcentrica(M0, exc);
if (E == pi) ret0 = pi;
elseif (E < pi) ret0 = 2*atan(sqrt((1+exc)/(1-exc))*tan(E/2));
elseif (E > pi) E = 2*pi-E; ret0 = 2*(pi - atan(sqrt((1+exc)/(1-exc))*tan(E/2)));
endif
retv(i) = ret0 + n*2*pi;
endfor
endfunction
#{
Anomalía media correspondiente a una anomalía verdadera dada. Función inversa de anomaliaVerdadera().
#}
function retv = MdeAnomaliaVerdadera (nu, exc)
retv = zeros(1,length(nu));
for i = [1:length(nu)]
n = sign(nu(i))*abs(floor(nu(i)/(2*pi)));
nu0=nu(i)-n*2*pi;
if (nu0 == pi) E = pi;
elseif (nu0 < pi) E = 2*atan(sqrt((1-exc)/(1+exc))*tan(nu0/2));
elseif (nu0 > pi) E = 2*(pi - atan(sqrt((1-exc)/(1+exc))*tan((2*pi-nu0)/2)));
endif
M = E - exc * sin(E);
retv(i) = M + n*2*pi;
endfor
endfunction
#{
Devuelve 'y' (alfa) Ascension Recta de un punto en la eclíptica con Longitud Eclíptica 'x' (lambda)
y una inclinación 'incli' de la ecliptica.
Por tanto x medida desde el punto de Aries
La diferencia x-y es una función periodica de periodo pi, impar respecto a 0, par respecto a pi/4.
Si x = X+n*pi, con 0<=X<=pi
x-y(x) = X-y(X) --> y(x)=y(X)+n*pi , n = sign(x)*abs(floor(x/pi))
#}
function retv = ARdeLE(xv, incli)
retv = zeros(1,length(xv));
for i = [1:length(xv)]
x = xv(i);
n = sign(x)*abs(floor(x/pi));
x0=x-n*pi; # x0 es X
ret = acos(cos(x0)/sqrt((cos(x0))^2+(sin(x0)*cos(incli))^2)) + n*pi;
retv(i)=ret;
endfor
endfunction
#{
DeClinación (delta) de un punto con Longitud ecliptica 'x' (lambda), para inclinación 'incli' de la eclíptica.
sin(delta)=sin(lambda)*sin(incli)
#}
function retv = DCdeLE(xv, incli)
retv = zeros(1,length(xv));
for i = [1:length(xv)]
x = xv(i);
ret = asin(sin(x)*sin(incli));
retv(i)=ret;
endfor
endfunction
EDTcalculo_principal.txt
#invocada desde EDTinvocarTodo.txt
#{
d: tiempo medido en dias solares medios, desde el 1 de enero de 2009 (d=0 a las 0h de ese día)
sufijo _e para valores en el equinoccio de marzo y sufijo _p para valores en el perihelio
nu anomalía verdadera del Sol, medida en sistema orbital, origen en el perihelio
L Longitud eclíptica del Sol, medida en sistema equinoccial, origen en el punto de Aries
AR_Sol ascension recta del Sol, medida en sistema equinoccial, origen en el punto de Aries
M anomalía media, medida en sistema orbtial, origen en perihelio. Unida al discurrir uniforme del tiempo, y a ECLI.
lamb longitud eclíptica de ECLI (igual en valor a la ascensión recta de ECUA), sistema equinoccial, origen en el punto de Aries.
AR_lamb ascensión recta de ECLI, sistema equinoccial, origen en el punto de Aries
#}
d_ini=-10; # incluiremos unos pocos dias del año anterior
d_fin=370; # y otros pocos del siguiente
dias=[d_ini:d_fin];
# En 2009 el equinoccio de primavera se producirá a las 11h 44m UT del 20 de marzo
d_e=31+28+19+((11+(44/60))/24);
# En http://aom.giss.nasa.gov/srorbpar.html obtenemos para la distancia angular desde el perihelio al nodo ascendente, en grados
AOM2009_gr = 283.05
# El angulo medido (en sistema orbital) desde el perihelio hasta el punto de Aries, en radianes,
nu_e = (360 - AOM2009_gr)*pi/180;
# A partir de este angulo determinamos cuando se pasa por el perihelio, d_p.
# Este angulo coincide con nu_e, la anomalia verdadera en el equinoccio de marzo, cuando el Sol pasa por el punto de Aries
# La anomalia media en el equinoccio es
M_e = MdeAnomaliaVerdadera(nu_e, excentricidadTierra);
# y M_e=(d_e-d_p)*omega_S de donde
d_p = d_e - (M_e/omega_S);
# anomalia media
M = omega_S*(dias-d_p);
nu_e = anomaliaVerdadera(M_e, excentricidadTierra);
nu = anomaliaVerdadera(M, excentricidadTierra);
# La diferencia angular en d= d_e entre ECLI y Sol en el S.R. orbital es igual a(M_e - nu_e),
# y coincide con la diferencia angular vista desde el S.R. equinoccial (lamb_e - L_e), siendo L_e=0
# Por tanto lamb_e es negativo, e igual a
lamb_e=M_e-nu_e
lamb_p = lamb_e + omega_T*(d_p - d_e);
# es importante recordar que lamb se refiere a ECLI visto en el S. R. Equinoccial, moviendose al ritmo omega_T.
lamb = lamb_e + omega_T * (dias - d_e);
# Precisamente en el S.R. Ecuatorial la AR (ascensión recta) de ECUA es igual a lamb de ECLI
AR_ECUA = lamb;
# La longitud ecliptica del Sol, L, seria (nu - nu_e) de no haber precesión. Pero como el equinoccio se mueve
# en sentido contrario al Sol, hay un pequeñisimo incremento de L adicional de modo que
L = nu - nu_e + omega_P * (dias - d_e);
L_e = 0;
L_p = 0 - nu_e + omega_P * (d_p - d_e);
#ascensión recta del Sol
AR_Sol = ARdeLE(L, incliECLI);
AR_Sol_e = ARdeLE(L_e, incliECLI);
AR_Sol_p = ARdeLE(L_p, incliECLI);
#ECUACION DEL TIEMPO EDT
valorEDT = (AR_ECUA - AR_Sol) * factorEDTminrad;
# ascensión recta de ECLI
AR_ECLI = ARdeLE(lamb, incliECLI);
#Ecuación de la inclinación de la eclíptica
valorEIE = -(AR_ECLI - AR_ECUA) * factorEDTminrad;
#Ecuación del centro o de la excentricidad de la órbita
valorEEX = -(AR_Sol - AR_ECLI) * factorEDTminrad;
EDTgrafica_EDT_EEX_EIE.txt
#invocada desde EDTinvocar_todo.txt
plot(dias, valorEDT,"-k;EDT;","linewidth",3, dias,valorEIE,"-b;EIE;",dias,valorEEX,"-r;EEX;",d_e,0,"+b",d_p,0,"+r");
xlabel("días desde el inicio del año 2009");
ylabel("minutos");
title("Gráfica 1 - ecuación del tiempo EDT");
grid("minor");
set (gca (), "xlim", [d_ini-5, d_fin+5]);
set(gca(),"position",[0.15,0.15,0.75,0.75])
legend("show","location","northwest")
set(text(36,1,"equinoccio"),"color","blue")
set(text(0,2,"perihelio"),"color","red")
fid = fopen ("c:/Octave/EDT/tabla_EDT_EEX_EIE.txt", "w");
fdisp(fid,"indice,d,fecha,EDT,EEX,EIE");
for i = [1:length(dias)]
fprintf(fid,"%d,%d,%s,%f,%f,%f\n",i,dias(i),datestr(datenum(2009,1,1)+dias(i),29),valorEDT(i),valorEEX(i),valorEIE(i));
endfor
fclose(fid);
EDTgrafica_lambda_alfa_gr.txt
#invocada desde EDTinvocar_todo.txt
lambd=[0:360];
alfa = ARdeLE(lambd*pi/180, incliECLI)*180/pi;
plot(lambd, lambd-alfa,"-k",0,0,"+k");
xlabel('{\fontsize{12} \lambda (grados)}');
ylabel('{\fontsize{12} \lambda - \alpha (grados)}');
title("Gráfica 2");
text(60,2.75,'{\fontsize{12}oblicuidad de la eclíptica = 23,439º}');
text(0,-0.25,'{\fontsize{12}punto de Aries}');
grid("minor");
set (gca (), "xlim", [-5, 365]);
set(gca(),"position",[0.15,0.15,0.75,0.75])
#print -dpng "c:/octave/EDT/grafica_lambda_alfa_gr.png";
fid = fopen ("c:/Octave/EDT/tabla_lambda_alfa_gr.txt", "w");
fdisp(fid,"lambda_gr,alfa_rad,lambda_rad,alfa_gr");
for i = [1:length(lambd)]
fprintf(fid,"%d,%f,%f,%f\n",lambd(i),alfa(i),lambd(i)*pi/180,alfa(i)*pi/180);
endfor
fclose(fid);
EDTgrafica_M_nu_gr.txt
#invocada desde EDTinvocar_todo.txt
M=[0:360];
nu = anomaliaVerdadera (M*pi/180, excentricidadTierra)*180/pi;
plot(M, M-nu,"-k",0,0,"+k");
xlabel('{\fontsize{12} M (grados)}');
ylabel('{\fontsize{12} M - \nu (grados)}');
title("Gráfica 3");
text(50,1.5,'{\fontsize{12}excentricidad = 0,016729}');
text(0,0.2,'{\fontsize{12}perihelio}');
grid("minor");
set (gca (), "xlim", [-5, 365]);
set(gca(),"position",[0.15,0.15,0.75,0.75])
#print -dpng "c:/octave/EDT/grafica_M_nu_gr.png";
fid = fopen ("c:/Octave/EDT/tabla_M_nu_gr.txt", "w");
fdisp(fid,"M_gr,nu_rad,M_rad,nu_gr");
for i = [1:length(M)]
fprintf(fid,"%d,%f,%f,%f\n",M(i),nu(i),M(i)*pi/180,nu(i)*pi/180);
endfor
fclose(fid);
EDTgrafica_EDT_DiaSolar.txt
#invocada desde EDTinvocar_todo.txt
difer = zeros(1,length(dias));
for i = [2:length(difer)]
difer(i)=valorEDT(i)-valorEDT(i-1);
endfor
difer(1)=difer(366);
difer=-difer*60;#diferencia dia a dia en segundos CAMBIADA DE SIGNO
diasEnMes=[31,28,31,30,31,30,31,31,30,31,30,31];
nombreMes=["Ene","Feb","Mar","Abr","May","Jun","Jul","Ago","Sep","Oct","Nov","Dic","Ene"];
diaIniMes=[0,cumsum(diasEnMes)];
subplot(2,1,1);
plot(dias, valorEDT,diaIniMes,valorEDT(-d_ini+1+diaIniMes),'+');
set (gca (), "xlim", [d_ini-5, d_fin+5]);
ylabel("EDT (minutos)");
#set(text(50,18,"ecuación del tiempo"),"color","black");
for i=[0:12] set(text(diaIniMes(i+1)-4,valorEDT(-d_ini+1+diaIniMes(i+1))+5,nombreMes(3*i+1:3*i+3)),"color","black") ;endfor
grid("on");
subplot(2,1,2);
plot(dias,difer,diaIniMes,difer(-d_ini+1+diaIniMes),'+');
set (gca (), "xlim", [d_ini-5, d_fin+5]);
xlabel("días desde el inicio del año 2009");
ylabel(strcat('\Delta D_v (segundos)'));
set(text(52,26,"exceso del día solar verdadero sobre el día solar medio"),"color","black")
set(text(52,23,"valores positivos: días más largos, negativos: días más cortos"),"color","black")
for i=[0:12] set(text(diaIniMes(i+1)-4,difer(-d_ini+1+diaIniMes(i+1))-5,nombreMes(3*i+1:3*i+3)),"color","black") ;endfor
grid("on");
fid = fopen ("c:/Octave/EDT/tabla_EDT_DiaSolar.txt", "w");
fdisp(fid,"indice,d,fecha,EDT_min,difer_s");
for i = [1:length(dias)]
fprintf(fid,"%d,%d,%s,%f,%f\n",i,dias(i),datestr(datenum(2009,1,1)+dias(i),29),valorEDT(i),difer(i));
endfor
fclose(fid);
EDTgrafica_analema.txt
#invocada desde EDTinvocar_todo.txt
#declinacion del Sol en grados
DC_Sol = DCdeLE(L, incliECLI)*180/pi;
DC_Sol_e = DCdeLE(L_e, incliECLI)*180/pi;
DC_Sol_p = DCdeLE(L_p, incliECLI)*180/pi;
# ángulo horario: diferencia angular entre la ascension recta del Sol y de ECUA, Horizontal, en grados
xH=(lamb-AR_Sol)*180/pi;
xH_e=(lamb_e-AR_Sol_e)*180/pi;
xH_p=(lamb_p-AR_Sol_p)*180/pi;
# plot(dias,DC_Sol);pause(2);#print -dpng "c:/octave/EDT/grafica_dias_DC_gr.png";
diasEnMes=[31,28,31,30,31,30,31,31,30,31,30,31];
nombreMes=["Ene","Feb","Mar","Abr","May","Jun","Jul","Ago","Sep","Oct","Nov","Dic","Ene"];
diaIniMes=[0,cumsum(diasEnMes)];
#plot(xH,DC_Sol,'-k',"linewidth",1,xH_p,DC_Sol_p,'+r',xH_e,DC_Sol_e,'+b')
latN=0 #latitud Norte del punto de observacion
plot(xH,DC_Sol+latN,'-k',"linewidth",1,xH_p,DC_Sol_p+latN,'+r',xH_e,DC_Sol_e+latN,'+b',xH(-d_ini+1+diaIniMes),DC_Sol(-d_ini+1+diaIniMes),'+g')
offx=[-1,-3,-3,-3,+1,+1,-3,-3,+1,+1,+1,+1];
offy=[-1.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5];
for i=[0:11] set(text(xH(-d_ini+1+diaIniMes(i+1))+offx(i+1),DC_Sol(-d_ini+1+diaIniMes(i+1))+offy(i+1),nombreMes(3*i+1:3*i+3)),"color","black") ;endfor
xlabel("Ángulo entre Sol y meridiano (grados)");
ylabel("Declinación del Sol (grados)");
title("Analema en el Ecuador");
grid("on");
#grid("minor");
set (gca (), "xlim", [-15, 15]);
set (gca (), "ylim", [-30+latN, 30+latN]);
set (gca (), "dataaspectratio", [1, 2, 1]);
set(gca(),"position",[0.15,0.15,0.75,0.75])
set(text(-9,0.5+latN,"equinoccio"),"color","blue")
set(text(-7,-23+latN,"perihelio"),"color","red")
set(text(10,0.5+latN,"OESTE"),"color","black")
set(text(-14,0.5+latN,"ESTE"),"color","black")
set(text(-2,27+latN,"NORTE"),"color","black")
set(text(-1,-27+latN,"SUR"),"color","black")
#print -dpng "c:/octave/EDT/grafica_analema.png";
pause(5);
#-----------------------------------------------------------------------------------
# grafica de los analemas a diferentes horas vistos desde una latitud no ecuatorial
source("c:/octave/EDT/EDTfunciones_cambio_coordenadas.txt")
lat=40; #latitud de la observacion
for i=[0:23]
[z,A]= zAhoriz(DC_Sol*pi/180,(xH+15*i)*pi/180,lat*pi/180);z=z*180/pi;A=A*180/pi;
zz{i+1}=90-z;AA{i+1}=A;#zz distancia al horizonte en vez de al cenit, en grados
endfor
plot(AA{1},zz{1},"k",AA{2},zz{2},AA{3},zz{3},AA{4},zz{4},AA{5},zz{5},AA{6},zz{6},AA{7},zz{7},AA{8},zz{8},AA{9},zz{9},AA{10},zz{10},AA{11},zz{11},AA{12},zz{12},AA{13},zz{13},AA{14},zz{14},AA{15},zz{15},AA{16},zz{16},AA{17},zz{17},AA{18},zz{18},AA{19},zz{19},AA{20},zz{20},AA{21},zz{21},AA{22},zz{22},AA{23},zz{23},AA{24},zz{24});
title("analema cada hora a 40º latitud Norte");
xlabel("Azimut desde el Sur (+ Oeste, - Este)(grados)");
ylabel("Altura sobre el horizonte (grados)");
grid("on");
set (gca (), "xlim", [-180, 180]);
set (gca (), "ylim", [-90, 90]);
#print -dpng "c:/octave/EDT/grafica_analemas40N.png";
pause(5);
#-----------------------------------------------------------------------------------
lat=-40; #latitud de la observacion
for i=[0:23]
[z,A]= zAhoriz(DC_Sol*pi/180,(xH+15*i)*pi/180,lat*pi/180);z=z*180/pi;A=A*180/pi;
zz{i+1}=90-z;AA{i+1}=A;#zz distancia al horizonte en vez de al cenit, en grados
endfor
plot(AA{1},zz{1},"k",AA{2},zz{2},AA{3},zz{3},AA{4},zz{4},AA{5},zz{5},AA{6},zz{6},AA{7},zz{7},AA{8},zz{8},AA{9},zz{9},AA{10},zz{10},AA{11},zz{11},AA{12},zz{12},AA{13},zz{13},AA{14},zz{14},AA{15},zz{15},AA{16},zz{16},AA{17},zz{17},AA{18},zz{18},AA{19},zz{19},AA{20},zz{20},AA{21},zz{21},AA{22},zz{22},AA{23},zz{23},AA{24},zz{24});
title("analema cada hora a 40º latitud Sur");
xlabel("Azimut desde el Norte (+ Oeste, - Este)(grados)");
ylabel("Altura sobre el horizonte (grados)");
grid("on");
set (gca (), "xlim", [-180, 180]);
set (gca (), "ylim", [-90, 90]);
#print -dpng "c:/octave/EDT/grafica_analemas40S.png";
pause(5);
#-----------------------------------------------------------------------------------
lat=0; #latitud de la observacion
for i=[0:23]
[z,A]= zAhoriz(DC_Sol*pi/180,(xH+15*i)*pi/180,lat*pi/180);z=z*180/pi;A=A*180/pi;
zz{i+1}=90-z;AA{i+1}=A;#zz distancia al horizonte en vez de al cenit, en grados
endfor
plot(AA{1},zz{1},"k",AA{2},zz{2},AA{3},zz{3},AA{4},zz{4},AA{5},zz{5},AA{6},zz{6},AA{7},zz{7},AA{8},zz{8},AA{9},zz{9},AA{10},zz{10},AA{11},zz{11},AA{12},zz{12},AA{13},zz{13},AA{14},zz{14},AA{15},zz{15},AA{16},zz{16},AA{17},zz{17},AA{18},zz{18},AA{19},zz{19},AA{20},zz{20},AA{21},zz{21},AA{22},zz{22},AA{23},zz{23},AA{24},zz{24});
title("analema cada hora en el ecuador");
xlabel("Azimut desde el Sur (+ Oeste, - Este)(grados)");
ylabel("Altura sobre el horizonte (grados)");
grid("on");
set (gca (), "xlim", [-180, 180]);
set (gca (), "ylim", [-90, 90]);
#print -dpng "c:/octave/EDT/grafica_analemasEcuador.png";
fid = fopen ("c:/Octave/EDT/tabla_analema.txt", "w");
fdisp(fid,"indice,d,fecha,difAR_gr,DC_gr,AR_Sol_gr,AR_ECUA_gr");
for i = [1:length(dias)]
fprintf(fid,"%d,%d,%s,%f,%f,%f,%f\n",i,dias(i),datestr(datenum(2009,1,1)+dias(i),29),xH(i),DC_Sol(i),AR_Sol(i)*180/pi,AR_ECUA(i)*180/pi);
endfor
fclose(fid);
EDTfunciones_cambio_coordenadas.txt
#{
paso de coordenadas ecuatoriales declinación delta, y ángulo horario t,
a coordenadas horizontales distancia cenital z y Azimut A, para una latitud lat
delta y t pueden ser vectores, pero de la misma dimensión. lat se considera escalar.
#}
function [z, A] = zAhoriz(delta, t, lat)
z = zeros(1,length(delta))';
A = zeros(1,length(delta))';
slat=lat;#valor original con signo
lat=abs(lat);#valor absoluto
for i = [1:length(z)]
if (slat<0) t(i)=t(i)+pi; #para latitudes negativas hay desfase pi en el angulo horario
endif
if (t(i)<0 || t(i)>2*pi)
t(i)=mod(t(i),2*pi); # reducimos SIEMPRE el ángulo horario t al intervalo [0,2*pi]
endif
z(i)=acos(sin(lat)*sin(delta(i))+cos(lat)*cos(delta(i))*cos(t(i)));
if (abs(z(i)) < 0.0001) sA=0; # para z=0 el valor de A es indefinido, elegimos A=0.
else sA=cos(delta(i))*sin(t(i))/sin(z(i)); # sA es sin(A)
cA=(-cos(lat)*sin(delta(i))+sin(lat)*cos(delta(i))*cos(t(i)))/sin(z(i)); #cA es cos(A)
endif
# para obtener A(i) en [0,2*pi]
# cuadrante coseno seno para angulo inverso usar
# 1 + + acos o asin
# 2 - + acos o pi-asin
# 3 - - 2*pi-acos o pi-asin
# 4 + - 2*pi-acos o 2*pi+asin
# En octave asin toma valores en [-pi/2,pi/2], y acos toma valores en [0,pi], para el dominio [-1,1].
if (sA>0) A(i)=acos(cA);
elseif (sA<0) A(i)=2*pi-acos(cA);
else A(i)=0;
endif
#Pero nos interesa A(i) en [-pi,pi]
if (A(i)>pi) A(i)=A(i)-2*pi;
endif
if (slat<0) z(i)=pi-z(i);
# ahora se deshace el desfase pi en latitudes negativas.
# Queremos seguir teniendo las 12h del mediodia a 0º de acimut, que ahora se cuenta desde el Norte, no desde el Sur
# y asi la grafica de analemas para latitudes sur queda bien
if (A(i)<=0) A(i)=A(i)+pi;
else A(i)=A(i)-pi;
endif
endif
endfor
endfunction
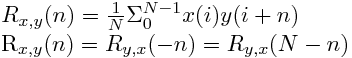 La primera línea es la definición, y la siguiente describe propiedades de simetría al intercambiar el orden de las funciones a correlacionar. Según esta definición para la correlación con n=10 de x con y, multiplico término a término los elementos de x con una copia de y desplazada a la izquierda 10 posiciones. x(1) se multiplica con y(1+10), etc.
La primera línea es la definición, y la siguiente describe propiedades de simetría al intercambiar el orden de las funciones a correlacionar. Según esta definición para la correlación con n=10 de x con y, multiplico término a término los elementos de x con una copia de y desplazada a la izquierda 10 posiciones. x(1) se multiplica con y(1+10), etc.











